Tamentai - Multiple faces Reference Charts
Creating multiface markings focuses on sub-dividing either the main triangle or the main diamond that results from the original C10 division into smaller segments that create either original or off-set concentric pentagons expanding outward from the 10-combination division centers. How many segments the sides of the triangle or diamond are divided into during this process determines how many additional hexagons will be added around the 10-pt centers as the threads are laid down. Thankfully, we don't have to sit and diddle out which main shape of the original 10-combination we need to divide into how many segments in order to get so many centers; it's been tabulated for us. Once can also reverse the process and determine how many faces are on a marked temari. Not only are references available to create these markings - so too can they be analyzed to determine how many faces are on a completed ball.
You'll find many such reference charts in many temari books. These are compiled through various resources and Ai's lessons.
| 10 Combination Standard Division/ 6-Part Triangle: | |||||||||||||||||||||||||
|
Formula for finding number of imperfect centers: (1/3X²) x 10 + 2 = # of imperfect centers using 6part Triangle, where X is the number side AB is being divided by (remember, must be a multiple of 3). (To clarify the formula: multiple X times X, then divide by 3. Multiply that result by 10. Add 2.) For example: If Triangle side is divided by 6: 6 times 6 = 36; divide 36 by 3 = 12; multiply by 10 = 120; add 2 = 122 |
||||||||||||||||||||||||
| Formula for finding number of perfect
centers: X² x 10 + 2 = # of perfect centers using 6 part
Triangle, where X is the number side AB is being divided by
(must be multiple of 3). (To clarify the formula: Multiple
X times X, then multiple that result by 10; to that result add
2). For example: If Triangle side is divided by 6: 6 times 6 = 36; multiply 36 by 10 = 360; add 2 to 360 = 362 |
|||||||||||||||||||||||||
| 10 Combination Standard Division / 4-Part Diamond: | ||||
| Divide 4-Part Diamond: |
Formula for finding
number of imperfect centers: X² x 10 + 2 = # of imperfect
centers using 4-part Triangle, where X is the number side AC is
being divided by. (To clarify the formula: multiple X times X, then multiply by 10, to that result add 2.) For example: If Diamond side is divided by 6: 6 times 6 = 36; multiply 36 by 10 = 360, add 2 = 362. -------------------------------------
Formula for finding number of perfect centers: X² x 30 + 2 = # of perfect centers using 4 part Diamond, where X is the number side AC is being divided by. (To clarify the formula: Multiple X times X, then multiple that result by 30; to that result add 2). For example: If Diamond side is divided by 6: 6 times 6 = 36; multiply 36 by 30 = 1080; add 2 to 1080 = 362 |
|||
| # segments |
Incomplete / Imperfect Centers |
Complete / Perfect Centers |
||
| 1 |
12 |
32 |
||
| 2 |
42 |
122 |
||
| 3 |
92 |
272 |
||
| 4 |
162 |
482 |
||
| 5 |
252 |
752 |
||
| 6 |
362 |
1082 |
||
| 7 |
492 |
1472 |
||
| 8 |
642 |
1922 |
||
| 9 |
812 |
2432 |
||
| 10 |
1002 |
3002 |
||
| 11 |
1212 |
3632 |
||
| 12 |
1442 |
4322 |
||
| 13 |
1692 |
5072 |
||
| 14 |
1962 |
5882 |
||
| 15 |
2252 |
6752 |
||
| 16 |
2562 |
7682 |
||
| 17 |
2892 |
8672 |
||
| 18 |
3242 |
9722 |
||
| 19 |
3612 |
10,832 |
||
| 20 |
4002 |
12,002 | ||
Determining the Number of Faces: To reverse the process and determine the number of faces that are on a marked ball, first locate the original 10-pt pentagon centers from the original 10-Combination marking. Choose 2 adjacent pentagons, labeled 1 and 2 in the diagrams below:
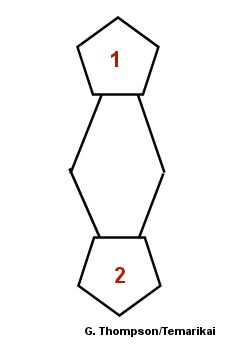 |
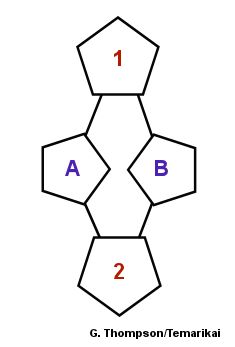 If, as a line taken from one center down vertically to the adjacent one (1 to 2), there are no pentagons pointing in towards the middle (as in diagram to the left) on the short-axis, the marking is worked on the 4-part diamond subset. If there is a set of pentagons pointing towards the middle on the short axis, as shown in the diagram to the right, then the marking is worked off of the 6-part triangle subset. Then, count the number of hexagons running in the vertical line from the sides of Pentagons 1 & 2. Use this value and the table below to determine the number of faces. |
| 6- Part Triangle | 4- Part Diamond | |||
| #
Hexagons |
Faces |
#
Hexagons |
Faces |
|
| 2 | 32 | 1 | 42 | |
| 5 | 122 | 2 | 92 | |
| 8 | 272 | 3 | 162 | |
| 11 | 482 | 4 | 252 | |
| 14 | 752 | 5 | 362 | |
| 6 | 492 | |||
| 7 | 642 | |||
| 8 | 812 | |||
Lessons and translations (with deep
appreciation): Ai M.
Direct translation and translation assistance: Milly K., Kiyoko T.;
Publications: Kaga Hana Temari (ISBN4-8377-0292 -9), Sosaku Temarizikushi (ISBN4-8377-0696-7),
Shugyoku no Azuma Temari (978-4837701088), Edo Temari (ISBN4-8377-0394-1)
Direct translation and translation assistance: Milly K., Kiyoko T.;
Publications: Kaga Hana Temari (ISBN4-8377-0292 -9), Sosaku Temarizikushi (ISBN4-8377-0696-7),
Shugyoku no Azuma Temari (978-4837701088), Edo Temari (ISBN4-8377-0394-1)
This is a TemariKai.com Printable Page; © 2014, all rights
reserved. Right click to print one copy for personal use.
Last updated 2/2015 © 1998 - 2015 TemariKai.com, G. Thompson/PuffinStuff, Inc.
